The Basic Idea: Cipher of Ciphers
A very simple and basic polymorphic cipher requires a crypto engine which
can choose from let's say four 128 bit encryption algorithms,
e.g. AES Rijndael, AES Twofish, RC6 and Mars. Each of these base ciphers
is regarded as "unbreakable" by most experts these days.
A 130
bit key is used to encrypt messages - 2 bit select one of the four
available base ciphers and the remaining 128 bit represent the key for
the chosen base cipher. The result is an unbreakable 130 bit cipher as
each of the 128 bit base ciphers is unbreakable and each base cipher
generates ciphertext with very good pseudo-randomness and thus cannot be
identified by its output bit pattern.
The two
additional bits make the proposed "Cipher of Ciphers" stronger than each
of the base ciphers with the following advantages:
1. The Brute Force Attack takes longer on 130bit than on 128 bit
2.
The two additional bits consume only once a little CPU time while they
don't eat up any time when encrypting the next 100 terabytes e.g. when
used in server-to-server communication
3. An attacker must try
to crack four base ciphers instead of one.
Weenies might try to argue
against this by saying "if I crack AES Rijndael, I can already crack 25%
of all encrypted messages". This is true.
But using just 4 base
ciphers isn't all that great. What if a more powerful polymorphic cipher
would feature a set of 128 base ciphers? Cracking one of them would
expose less than 1% of all encrypted messages. Cracking one of the base
ciphers is although likely to be just as difficult as cracking AES Rijndael.
What if the password would compile into a cipher?
What if block size was heavily variable?
Encryption is supposed to be
frustrating for attackers. This is the latest Polymorphic Cipher:
The Giant Block Size Polymorphic Cipher
A 256megabyte implementation of the Giant Block Size Polymorphic Cipher is available in the Windows software "File Encryption in One Block".
White paper about the  Giant Block Size Polymorphic Cipher (PDF, 2.6MB)
Giant Block Size Polymorphic Cipher (PDF, 2.6MB)
Why are encryption algorithms like AES, Twofish, DES, etc. limited to 64 or 128 bit block size?
Why is the key setup time extremely short (a few nanoseconds only)?
Why can over one million AES blocks be placed and operated on a single 8'' silicon wafer?
Why do government organizations that are in place to to spy on people only promote such tiny encryption algorithms?
Those who don't like to hear such questions are free to leave this website at any time and go on in trusting Santa Claus.
If you are although interested in reading something new, you might find interesting stuff on this website. Here's a very beautiful photo of a silicon wafer that was recently manufactured. Since it is possible to place 50 billion transistors and one million AES codebreaking chips on 8'' silicon wafers like the one shown below, the need for ciphers with much larger keyspace and block size is indicated.

Modern ciphers should make the task of breaking codes much more difficult for attackers. Here's a list of requirements that must be met:
|
Design goal
|
Polymorphic Giant Block Size Cipher
|
Conventional Ciphers
|
|
Large and variable block size
|
Block size is only limited by the resources of the target computer(s). Target systems should run at 500MHz or higher and more than 10Mbyte free RAM should be available. The Strict Avalanche Criterion is thus met perfectly.
|
Not supported at all. Ciphers like AES need little more than 1Kbyte of machine code and a microcontroller typically used in cheap smart cards and washing machines (approx. 20.000 transistors) to run. It is conceivable that such conventional ciphers could have been hardened against all kinds of attacks if more complex implementtations would have been the target.
|
|
No padding to reach block granularity shall be necessary
|
Block size is totally variable and blocks keep their length => no padding required, which results in no information being transmitted in vein.
|
DES: 8 byte block granularity,
AES: 16 byte block granularity
ð Padding required
A 2048 bit conventional block cipher would require padding to 256 byte blocks resulting in dramatic increase in data traffic if used for the encryption of TCP or UDP data packets.
|
|
Partitioning of extremely big blocks at arbitrary position
|
Blocks that are too big to handle are truncated into sub-blocks with block sizes that are determined by the key as well as the length of the original block.
|
Not supported at all. AES, DES and all other well-known block ciphers feature fixed block sizes.
|
|
Resistance against all known attacks
|
Due to its variable nature are Polymorphic Ciphers not susceptible to typical attacks that target specific characteristics and/or known weaknesses of fixed ciphers. Brute Force is although applicable to any cipher.
|
AES can be broken easily by DPA (Differential Power Attack) on small microprocessors and microcontrollers.
|
|
Resistance to future attacks that may cut effective key size by ½ or even 2/3
|
Cutting of effective key size by ¾ would result in still extremely high complexity of O(2256) or higher, which is regarded as totally safe for the next trillion years.
|
Cutting of effective key size by ½ results in an extremely low complexity of 264. The cipher would be regarded as being broken.
|
|
Extremely long key setup time
|
> 100ms on a modern microprocessor make comparably short keys safe against Brute Force attacks conducted on a few machines. Extremely long key setup time increases energy consumption multiplied by the time needed for Brute Force by factor 2.000.000.
|
<1µs help attackers to try each and every password combination. This is highly dangerous if short passwords are being used to protect data.
|
|
Platform independence
|
Runs on any 32 or 64 bit microprocessor or microcontroller
|
Runs on any 8-, 16-, 32- and 64 bit microprocessor and microcontroller
|
|
Polymorphism and data dependent selection of functions
|
The cipher is not only completely variable, but also is the block size huge and unpredictable if truncation is performed. No static weakness is exhibited.
|
Classic ciphers are static and can thus be thoroughly reverse-engineered and analyzed. Cryptanalysis of a mechanism that does always exactly the same is somewhat easier than for a mechanism that never executes the same operation twice.
|
|
Use of large amounts of resources
|
1 Mbit internal state requires at least approx. 8 million transistor equivalents to run. This alone makes Brute Force Attack more difficult and much more expensive compared with conventional ciphers.
|
Less than 50.000 transistor functions are required to build an AES block. Approx. 1.000.000 AES blocks can run in parallel on an 8’’ wafer to try and break a code using Brute Force.
|
|
Attacks need to be expensive for an attacker
|
The proposed cipher requires a lot of resources and extremely much time for key setup, an attacker requires a “time x resources product” of approx. 200.000 times compared with AES Rijndael when using keys with a similar length.
|
Trying different AES keys requires 50.000 transistor equivalents and less than 1µs. This isn’t really all that much. This is a REAL weakness.
|
|
High speed
|
1500 Mbit/s on an Intel Core i7 950 (3.06GHz) (64 bit C++ code, 1024 byte block length)
|
1000 Mbit/s on an Intel Core Core i7 950 (3.06GHz) (64 bit C++ code)
|
|
Proven security
|
Three round Luby Rackoff features proven security (the mathematical proof is contained in the PDF doc that describes the cipher); polymorphic encryption is increasingly popular among experts but it’s probably impossible to prove security of the entire cipher.
|
Security is not proven. Extensive peer review indicates that the cipher could be broken in the future:
For 128-bit Rijndael, the problem of recovering the secret key from one single plaintext can be written as a system of 8000 quadratic equations with 1600 binary unknowns.
Recently has a new related-key boomerang attack on the full AES-192 and the full AES-256 been found by Biryukov and Khovratovich. A 256 bit key is reduced to a 119 bit key when using AES-256. The attack is not applicable to 128 bit keys.
|
Highly variable block size of the Giant Block Size Polymorphic Cipher
The Giant Block Size Polymorphic Cipher features a block size of 128 to 1 megabit in the standard compilation of the demo C++ project. Maximum block size is although only limited by the resources of the target machine. For a PC, block sizes of 500 megabyte or more are possible.
The advantage of having a huge (and variable) block size is evident when looking at the following photos:
1. Original image (scaled down to 40%)

2. AES encrypted image in ECB mode (scaled down to 40%)

3. Image encrypted with Giant Block Size Polymorphic Cipher with 1.6 megabyte block size in ECB mode (scaled down to 40%)

The result obviously speaks for itself. It is almost impossible to use the cipher in a totally wrong way.
Large keyspace of the Giant Block Size Polymorphic Cipher
Why only using short keys? Many ciphers that have been broken featured relatively short keys. There is simply no need for economizing here. Those who said that it will always be impossible to break DES are in many cases the same who say today that AES cannot be broken. They might be right. But what if they were wrong?
The Giant Block Size Polymorphic Cipher has a variable keyspace. Minimum key size is 1024 bit. Maximum keysize extends beyond 6144 bit.
The Strict Avalanche Criterion (SAC)
When cryptographers claim to have taken the avalanche criterion into account, they usually don’t (want to) realize that this is mathematically impossible with block sizes around 128 or 256 bit as the messages that are encrypted with those ciphers are typically much longer. A cipher that satisfies the Strict avalanche Criterion is one for which just one change in a single bit makes approx. 50% of the bits in a block change their state.
Even typical TCP or UDP packet sizes of only 1Kbyte equal 64 times 16 bytes (128 bits = 16 bytes). The example of an IPv4 packet clearly demonstrates that with only 128 bit block length, almost the entire header of all IP packets with identical length is encrypted into the same ciphertext:
|
bit offset
|
0–3
|
4–7
|
8–15
|
16–18
|
19–31
|
|
0
|
version
|
header length
|
differentiated services / type of service
|
total length of packet
|
|
32
|
identification
|
flags
|
fragment offset
|
|
64
|
time to live
|
protocol
|
header checksum
|
|
96
|
source IP address
|
|
128
|
destination IP address
|
|
160
|
data (if there are no options – otherwise options are inserted before data)
|
If the data area does not contain any block counter, even more static ciphertext will be created. The mapping would be much better if block length of the cipher would at least span up to the first few bytes of the payload. IPv6 headers are even more critical. A cipher with fixed block length of 512 bit would be required to yield a relatively useful mapping! At this point it must be pointed out that “popular” ciphers are always those that have been certified by authorities whose job mainly consists of gathering intelligence. There is a clear conflict of interests for these government organizations. These professionals clearly know about the blatant deficiencies of the encryption algorithms that they certify and then promote.
Variable block length
While conventional block ciphers with large but fixed block lengths of e.g. 8192 bit suffer from their coarse granularity, this is not the case for a cipher with variable block length. If the task was to encrypt 1100 bytes of UDP traffic using an 8192 bit block cipher, the designer of a communication system using this conventional cipher would have only one choice:
As 1100 byte can only be encrypted in 1024 byte chunks ( due to the 8192 bit block length), this data would have to be transmitted in two separate data packets with 1024 byte length. The first packet would contain the first 1024 bytes, while the second packet would contain the remaining 76 bytes + 948 bytes of totally useless padding information. It is not even possible to send all 2048 byte in one data packet simply because MTU size for Ethernet is 1500 byte and for PPPoE it is even less or equal 1492 byte!
The proposed cipher although encrypts the entire 1100 byte in one packet without changing the size of the packet.
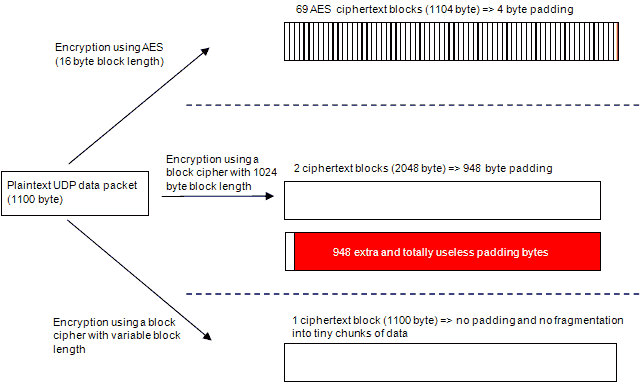
This example clearly demonstrates one of the most decisive advantages of the proposed class of ciphers – block ciphers featuring large block lengths must be designed to avoid block granularity. Encryption of remaining data could very well be performed by using a cipher with a smaller block size, but it is definitely favourable to encrypt the entire block at once. The figure above further reveals that typical AES-encrypted IP data packets are highly fragmented!
High speed of the Giant Block Size Polymorphic Cipher
Even at large block lengths is the Giant Block Size Polymorphic Cipher 50% faster than AES with its tiny block length of 16 byte (128 bit) ! Speed of 1.5 gigabit per second was measured at 1024 bit block length with 64 bit C++ code on an Intel Core i950 microprocessor. The cipher is thus perfectly suited for the encryption of TCP- or UDP data packets for internet television (IP TV), VoIP, Desktop Sharing or other streaming media applications for which cost per transmitted data packet is of importance. Especially for IP TV and Desktop Sharing applications is the investment into this extraordinary cipher quickly written off and money is subsequently made for many years.
Key Setup of the Giant Block Size Polymorphic Cipher
During the key setup phase is the key expanded for use by all sub-functions that require keying. This applies to:
- Confusion sequence generators for the Initial Permutation IP step,
- Shared (and constant) Internal State of the round functions,
- Initial Internal State of the round functions.
Fast Polymorphic PRNG (PseudoRandom Number Generator) functions can be designed to require an enormous amount of random access memory – for the Internal State as well as for the polymorphic sequence. It is desirable that this pseudorandom data, which is derived from the key, is computed in a lengthy, irreducible number of operations. Another design goal is the irreducible usage of as much RAM as appropriate for the class of target computers the final application program running the cipher actually runs on. For PCs, RAM usage of 1 to 10 Megabytes is very well tolerated by users. Internal State of such size forces an opponent who tries different and possibly likely keys to invest in a lot of chip space and in the electric power to operate 8 .. 80 million transistors. Computing and loading 10 Megabytes of pseudorandom data requires at least 1 million clock cycles. This compares with only 52 bytes of Internal State for the AES Rijndael algorithm that is computed within less than 1000 machine instructions (less than 500 machine instructions on many 32 bit microprocessors). The AES algorithm can be implemented in just a little more than 1Kbyte of machine code and approx. 20.000 transistors, if a very basic CPU is used as target.
Design of the Giant Block Size Polymorphic Cipher
The Polymorphic Giant Block Cipher features a provably secure structure with key dependence in all variable parts of the structure. The enciphering operation is further dependent on the block size that can vary greatly. The cipher has the tendency to take advantage of big blocks whenever this is possible. The cipher is a substitution-permutation network operating on a minimum of 128 bit words (16 bytes) and a maximum of bits allowed by the target application and target platform, thus giving an almost arbitrary block size. Block size can thus easily exceed 1Mbyte on a commercial personal computer! The default setting for the maximum block size of the demonstration implementation is 128 kbyte in order not to exceed the cache size of the secondary cache of modern 64 bit microprocessors.
The proposed encryption is E=DM o F1 o F2 o F3 , where DM is a decorrelation module and Fi is one Luby-Rackoff (Feistel) round with a keyed pseudorandom function as round function.
For more information please follow the link to the white paper about the Giant Block Size Polymorphic Cipher (PDF, 2.6MB)